Interpretations

A map changes input structures to output structures. Another way to think about it is that, under a map, an output structure is some reflection of the input structure.

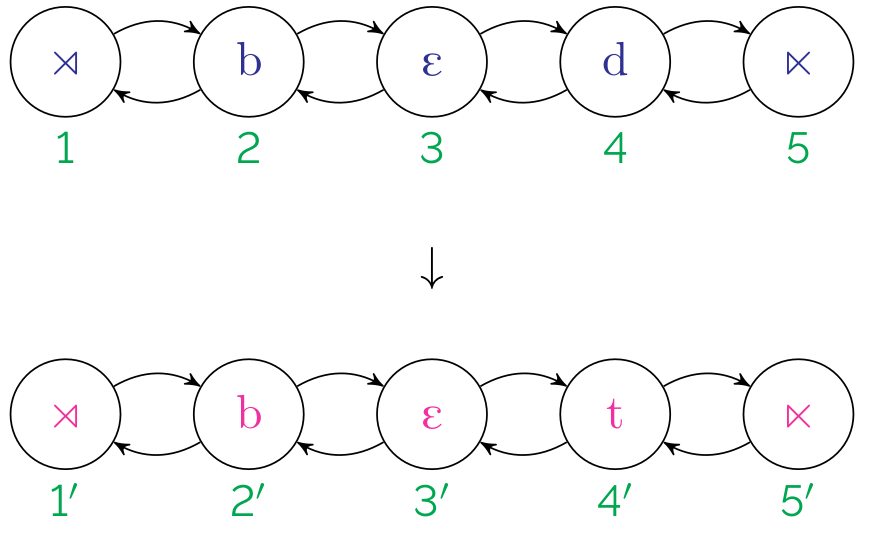
Interpretations specify maps by defining output structures in terms of the input structures (Engelfriet and Hoogeboom, 2001).

A scheme is thus a series of definitions of (output) properties. A boolean monadic recursive scheme is thus a scheme in which each property in the scheme is boolean (i.e., returns a boolean value) and monadic (i.e. unary), and the definitions are recursive (i.e., the properties being defined can be used in their own definitions).

In phonological terms, output formulas assert the conditions under which a segment is \(+\) for a given feature in the output structure.

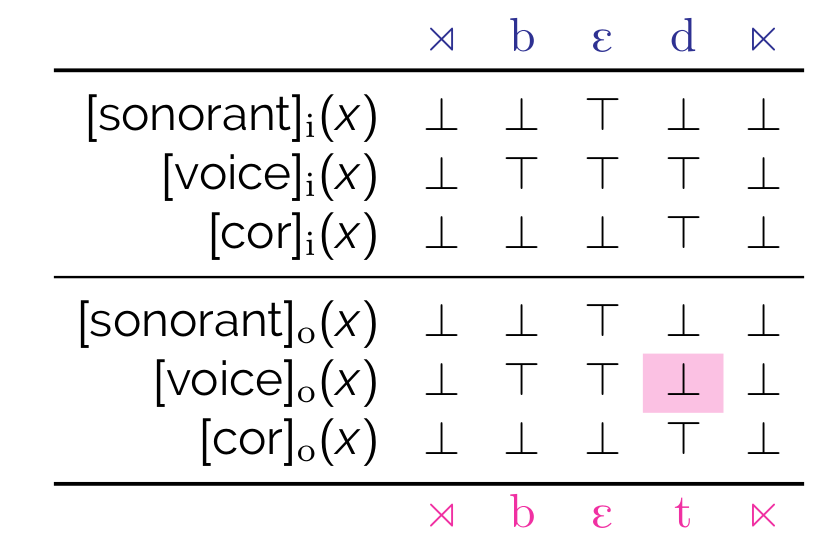
Thus, a BMRS for word-final devoicing is as follows:

\[ \begin{array}[t]{ll} [\mathrm{son}]_o(x) := [\mathrm{son}]_i(x) \\ [\mathrm{voi}]_o(x) := \mathtt{if}~\mathrm{D\#}_i(x)~\mathtt{then}~\bot~\mathrm{else}~[\mathrm{voi}]_i(x)\\ [\mathrm{cor}]_o(x) := [\mathrm{cor}]_i(x) \\ \end{array} \]

This obtains the truth value table above.