Logical language

The core of BMRS syntax are expressions of the form

\[\mathtt{if}~A~\mathtt{then}~B~\mathtt{else}~C\]

that return boolean values (\(\top\) or \(\bot\))

For example,

\[ \mathtt{if}~[\mathrm{son}]_i(x)~\mathtt{then}~\bot~\mathtt{else}~[\mathrm{voi}]_i(x) \]

...is \(\top\) iff \(x\) is a voiced obstruent, as shown below.

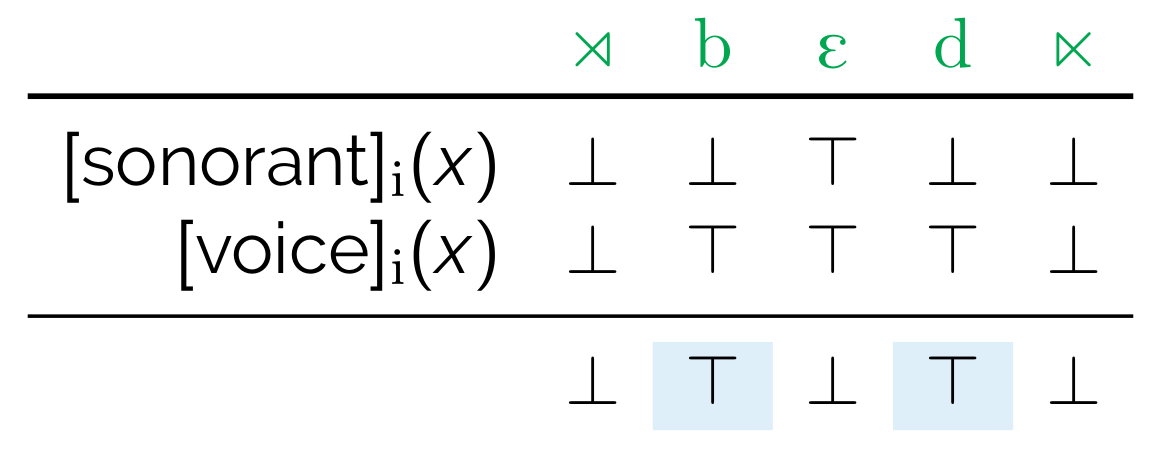
Furthermore, \(A\), \(B\), or \(C\) can be another expression. Usually this is \(C\), to chain together expressions, as in

\[ \begin{array}[t]{l} \mathtt{if}~[\mathrm{son}]_i(x)~\mathtt{then}~\bot~\mathtt{else}~\\ \mathtt{if}~[\mathrm{voi}]_i(x)~\mathtt{then}~\top~\mathtt{else}~\bot \end{array} \]

As is perhaps obvious at this point, expressions define properties. For example, we can explicitly define what it means to be a voiced obstruent using the expression above.

\[\left[\begin{array}{l}-\mathrm{son}\\+\mathrm{voi}\end{array}\right]_i(x):=\mathtt{if}~[\mathrm{son}]_i(x)~\mathtt{then}~\bot~\mathtt{else}~[\mathrm{voi]_i(x)}\]

Or what it means to be word-final.

\[ \mathrm{final}_i(x):=\mathtt{if}~\ltimes(s(x))~\mathtt{then}~\top~\mathtt{else}~\bot \]

And then what it means to be a word-final voiced obstruent.

\[ \mathrm{D\#}_i(x):=\mathtt{if}~\left[\begin{array}{l}-\mathrm{son}\\+\mathrm{voi}\end{array}\right]_i(x)~\mathtt{then}~\mathrm{final}(x)~\mathtt{else}~\bot \]